Quiz de prérentrée

Primary tabs

Question 1

Quel est le domaine de définition dans

$\mathbb{R}$ de la fonction suivante :

$\dfrac{x-1}{e^x-2}$

Catégorie:

Domaine de définition

Votre réponse	Choix	Commentaire	Bonne réponse
	$\mathbb{R}$
	$\mathbb{R} \setminus \{ \ln(2) ; 1 \}$
	$\mathbb{R} \setminus \{ 1 \}$
	$\mathbb{R} \setminus \{ \ln(2) \}$

Question 2

Quel est le domaine de définition dans

$\mathbb{R}$ de la fonction suivante :

$\dfrac{x-5}{\ln(x-2)-1}$

Catégorie:

Domaine de définition

Votre réponse	Choix	Commentaire	Bonne réponse
	$\rbrack -2 ; \mathrm{e}-2 \lbrack \; \cup \; \rbrack \mathrm{e}-2 ; 5 \lbrack \; \cup \; \rbrack 5 ; +\infty \lbrack$
	$\mathbb{R} \setminus \{ \mathrm{e}-2 \}$
	$\rbrack -2 ; +\infty \lbrack$	La valeur de $x$ qui annule le dénominateur doit être exclue du domaine de définition.
	$\rbrack -2 ; \mathrm{e}-2 \lbrack \; \cup \; \rbrack \mathrm{e}-2 ; +\infty \lbrack$

Question 3

Considérons un système général de 2 équations à 2 inconnues:

$\displaystyle (S)\begin{cases} a\times x + b\times y &= c\\ \alpha\times x + \beta\times y &= \gamma \end{cases}$
Soit

$E$ l'ensemble des solutions de

$(S)$ . Combien de solutions possibles peut comporter l'ensemble

$E$ ?

Catégorie:

Systèmes d'équations, inéquations, 2nd degré

Votre réponse	Choix	Commentaire	Bonne réponse
	Une infinité de solutions. Système lié.	$\displaystyle (S)\begin{cases} x - y &= 0\\ 2x - 2y &= 0\end{cases}$ $E=\left\{ ( x = t; y = t ) \mathrm{pour tout} t\in \mathbb{R} \right\}$
	Exactement deux solutions.
	Aucune solution. Système incompatible.
	Une seule solution. Système régulier.

Question 4

Considérons le système suivant :

$\displaystyle (S)\begin{cases} 2x+y & = 10 \\ 3x-y & = 5 \end{cases}$
Quelle est la valeur de la solution

$x$ ?

Catégorie:

Systèmes d'équations, inéquations, 2nd degré

Votre réponse	Commentaire	Bonne réponse
(10-y)/2		3

Question 5

La fonction

$x \mapsto x\sqrt{x}$ est dérivable en

$x=0$ .

Catégorie:

Continuité et dérivation

Votre réponse	Choix	Commentaire	Bonne réponse
	Vrai
	Faux

Revenir à la définition de la dérivée et calculer la limite en

$x=0$ de

$\lim\limits_{h\to 0 \\ h>0} \frac{(x+h)\sqrt{x+h}}{h}$ .

Question 6

Soit

$f$ une fonction numérique définie sur l'intervalle

$[-1;3]$ et

$a$ un réel de cet intervalle.
Si

$f$ est dérivable sur

$[-1;1]$ et sur

$[1;3]$ alors

$f$ est dérivable sur

$[-1;3]$ .

Catégorie:

Continuité et dérivation

Votre réponse	Choix	Commentaire	Bonne réponse
	Vrai
	Faux

La fonction dérivée

$f'(x)$ possède une dérivée à gauche et à droite de

$x=1$ , mais rien ne garantit que cette fonction

$f'(x)$ ne soit définie pour

$x=1$ .
C'est le cas dans le graphique ci-dessous.

Question 7

La fonction

$x \mapsto x\sqrt{x}$ est dérivable en

$x=0$ .

Catégorie:

Continuité et dérivation

Votre réponse	Choix	Commentaire	Bonne réponse
	Vrai
	Faux

Revenir à la définition de la dérivée et calculer la limite en

$x=0$ de

$\lim\limits_{\substack{h\to 0 \\ h>0}} \frac{(x+h)\sqrt{x+h}}{h}$ .

Question 8

La fonction dérivée de

$x \mapsto \sqrt{x^2 + 1}$ est toujours positive.

Catégorie:

Étude de fonctions

Votre réponse	Choix	Commentaire	Bonne réponse
	Vrai
	Faux

Quelles sont les limites en

$-\infty$ et

$+\infty$ ? La monotonie est-elle possible ?

Question 9

La fonction

$A$ définie et dérivable sur

$[0 ; 1]$ telle que, pout tout

$x$ de

$[0 ; 1]$ ,

$\displaystyle A'(x) = \frac{2x}{(1+2x)^2}$ est positive sur

$[0;1]$ .

Catégorie:

Étude de fonctions

Votre réponse	Choix	Commentaire	Bonne réponse
	Vrai
	Faux

La dérivée est positive, ce qui n'entraîne pas que la fonction soit positive. Essayer avec

$\displaystyle A = \frac{-1}{1+x^2}$ .

Question 10

Soit

$L$ une fonction définie et dérivable sur

$]0 ; +\infty [$ telle que pour tout réel

$x$ de

$]0; +\infty[$ ,

$L'(x) = \dfrac{1}{x}$ et

$L(1)=0$ .
Alors la fonction

$L$ est négative sur

$] 0 ; 1 [$ et positive sur

$]1 ; +\infty [$

Catégorie:

Étude de fonctions

Votre réponse	Choix	Commentaire	Bonne réponse
	Vrai
	Faux

À partir de l'énoncé, dresser le tableau de signe de

$L'$ en déduire le sens de variation de

$L$ en inscrivant la valeur de

$L(1)=0$ .

Question 11

Cette formule est-elle vraie ou fausse ?
Pour tous réels

$a$ et

$b$ ,

$e^{a+b}=\sqrt{e^{2a}e^{2b}}$ .

Catégorie:

Exponentielle

Votre réponse	Choix	Commentaire	Bonne réponse
	Vrai
	Faux

Revoir ses formules classiques :

$\sqrt{a\times b} = \sqrt{a}\times \sqrt{b}$

$\sqrt{X} = X^{\frac{1}{2}}$

$e^a\times e^b = e^{a+b}$

${e^a}^b = e^{a\times b}$

Question 12

Cette affirmation est-elle vraie ou fausse ?
Il existe un réel

$a$ et un réel

$b$ tels que

$2e^{a+b} = e^{2a} + e^{2b}$ .

Catégorie:

Exponentielle

Votre réponse	Choix	Commentaire	Bonne réponse
	Vrai
	Faux

Que se passe-t-il pour

$a=0$ et

$b=0$ ?

Question 13

La fonction

$f \colon x \mapsto e^{-x}$ est :

Catégorie:

Exponentielle

Votre réponse	Choix	Commentaire	Bonne réponse
	croissante sur $\mathbb{R}$ .	Ce n'est pas $e^x$ mais $e^{-x}$ . Calculer et étudier le signe de $f'(x)$ .
	décroissante sur $\mathbb{R}$ .
	négative sur $\mathbb{R}$ .

Question 14

Cette affirmation est-elle vraie ou fausse ?
Il existe un réel

$a$ et un réel

$b$ tels que

$e^{2a}+e^{2b} < 2e^{a+b}$ .

Catégorie:

Exponentielle

Votre réponse	Choix	Commentaire	Bonne réponse
	Vrai
	Faux

Étudier le signe puis développer l'expression

$\left( e^a - e^b\right)^2$ .

Question 15

L'inégalité

$\ln (x-1) < 1$ est vérifiée pour :

Catégorie:

Logarithmes

Votre réponse	Choix	Commentaire	Bonne réponse
	$x<1+e$	Prendre en compte le domaine de définition de $x \mapsto \ln (x)$ .
	$x>1$
	$1 < x < 1+e$

Question 16

Soit

$f$ la fonction définie par

$f(x)=\ln\left(x^2\right)$ .
L'ensemble de définition de

$f$ est :

Catégorie:

Logarithmes

Votre réponse	Choix	Commentaire	Bonne réponse
	$\mathbb{R}^*$
	$]0;+\infty [$
	$\mathbb{R}$

Question 17

L'inéquation

$e^x\leq 4$ a pour solution :

Catégorie:

Logarithmes

Votre réponse	Choix	Commentaire	Bonne réponse
	$\left] 0 ; 4 \right]$
	$\left] -\infty ; \ln(4) \right]$
	$\left] 0 ; \ln(4) \right]$

Question 18

Soit

$f$ la fonction définie sur

$]0 ; +\infty [$ par

$f(x)=x^2\ln(x)$ .
Le nombre dérivé de

$f$ en

$e$ est :

Catégorie:

Logarithmes

Votre réponse	Choix	Commentaire	Bonne réponse
	$0$
	$e^2$
	$3e$

Question 19

Voici la courbe des fréquences cumulées croissantes du nombre d'enfants moyen par famille en France en 2007.

Parmi les 4 affirmations suivantes, laquelle est correcte ?

Catégorie:

Statistiques

Votre réponse	Choix	Commentaire	Bonne réponse
	3 % des familles ont au plus 3 enfants.
	22 % des familles ont un enfant unique.
	90 % des familles ont au moins 2 enfants.
	70 % des familles ont au moins 1 enfant.

Pour trouver la fréquence des familles ayant un seul enfant, on fait le calcul

$0,7 - 0,48 = 0,22$ .

Question 20

Ce diagramme représente la répartition des élèves d'un lycée qui accueille 286 élèves en Seconde.

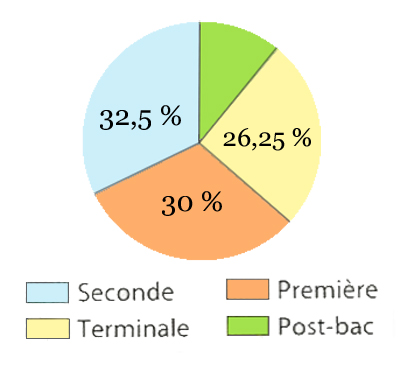
Quelle est la proportion

$\frac{post-bac}{première}$ ?

Catégorie:

Statistiques

Votre réponse	Choix	Commentaire	Bonne réponse
	$\frac{1}{3}$
	$\frac{3}{7}$
	On ne peut pas savoir.
	$\frac{3}{8}$

Le pourcentage d'élèves en post-bac est égal à

$100-(32,5+26,25+30) = 11,25 %$ .
La proportion demandée est donc

$\frac{11,25}{30}=0,375=\frac{3}{8}$ .

Main menu

Quiz de prérentrée

Primary tabs

Catégorie:

Catégorie:

Catégorie:

Catégorie:

Catégorie:

Catégorie:

Catégorie:

Catégorie:

Catégorie:

Catégorie:

Catégorie:

Catégorie:

Catégorie:

Catégorie:

Catégorie:

Catégorie:

Catégorie:

Catégorie:

Catégorie:

Catégorie: