On a représenté ci-contre les fréquences cumulées croissantes d'une série
statistique. Les fréquences ne sont pas en pourcentage. La somme totale des
fréquences est donc de 1.
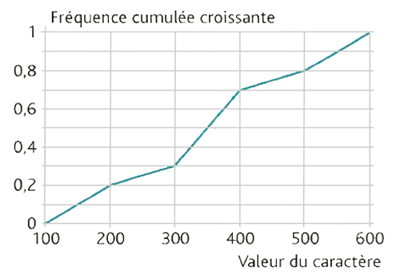
Une seule des 4 affirmations suivantes est vraie. Laquelle ?
| Votre réponse | Choix | Commentaire | Bonne réponse |
|---|
| $Me = 0,3$ | | |
| $Q_1=300$ | | |
| $Q_3 = 450$ | | |
| Aucune n'est vraie. | | |
Le troisième quartile noté $Q_3$ est une valeur qui coupe la population
en deux parts inégales : 3/4 (cad 75 %) ont un caractère inférieur à $Q_3$ et
1/4 supérieur à $Q_3$. Ici 75 % correspond à une fréquence de 0,75 , on se
place à 0,75 au niveau de l'axe des ordonnées (où se trouvent les fréquences
cumulées croissantes), on rejoint la courbe, et on lit l'abscisse
correspondante : cela donne la valeur de 450. qui est le troisième quartile.
Par la même méthode, on obtiendrait par exemple que le premier quartile est
d'environ 250 (on place cette fois 0,25 sur l'axe des ordonnées, on rejoint
la courbe, et on lit l'abscisse correspondante).