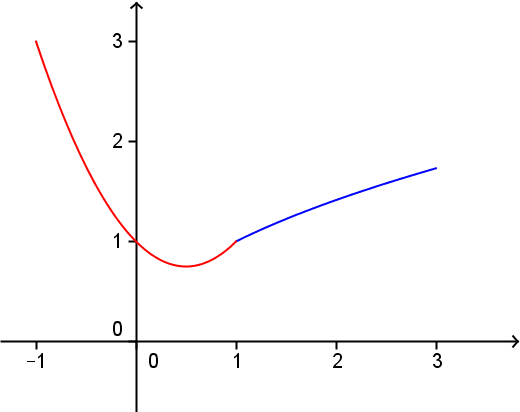
Soit $f$ une fonction numérique définie sur l'intervalle $[-1;3]$ et $a$ un réel de cet intervalle.
Si $f$ est continue sur $[-1;1]$ et sur $[1;3]$ alors $f$ est continue sur $[-1;3]$.
| Votre réponse | Choix | Commentaire | Bonne réponse |
|---|
| Vrai | | |
| Faux | | |
$f$ est définie sur l'intervalle $[-1;3]$.
De plus les deux intervalles $[-1;1]$ et $[1;3]$ se chevauchent.
Enfin, autour du point $x=1$, on pose $f(1)=a$, il ne reste qu'à comparer la limite à droite et à gauche de $f(x)$ avec la valeur de $f(1)=a$.