Quiz de prérentrée

Primary tabs

Question 1

Quel est le domaine de définition dans $\mathbb{R}$ de la fonction suivante : $\dfrac{x-5}{\ln(x-2)-1}$

Catégorie:

Votre réponseChoixCommentaireBonne réponse
$\rbrack -2 ; +\infty \lbrack$
Should not have chosen
$\rbrack -2 ; \mathrm{e}-2 \lbrack \; \cup \; \rbrack \mathrm{e}-2 ; 5 \lbrack \; \cup \; \rbrack 5 ; +\infty \lbrack$
Should not have chosen
$\rbrack -2 ; \mathrm{e}-2 \lbrack  \; \cup \; \rbrack \mathrm{e}-2 ; +\infty \lbrack$
Should have chosen
$\mathbb{R} \setminus \{ \mathrm{e}-2 \} $
Should not have chosen
Question 2

Quel est le domaine de définition dans $\mathbb{R}$ de la fonction suivante : $\dfrac{x-1}{x^2-2x+1}$

Catégorie:

Votre réponseChoixCommentaireBonne réponse
$\rbrack -\infty ; -1 \lbrack \; \cup \; \rbrack 1 ; +\infty \lbrack$
Should not have chosen
$\mathbb{R} \setminus \{ -1 \} $
Should not have chosen
$\mathbb{R}$
Should not have chosen
$\mathbb{R} \setminus \{ 1 \} $
Should have chosen
Question 3

À quel système correspond la région blanche du graphique ?

Catégorie:

Votre réponseChoixCommentaireBonne réponse
$\displaystyle{(S)\begin{cases} 2x+y & < 5\\ x-2y & > 8 \end{cases}}$
Should have chosen
$\displaystyle{(S)\begin{cases} 2x+y & < 5\\ x-2y & < 8 \end{cases}}$
Should not have chosen
$\displaystyle{(S)\begin{cases} 2x+y & > 5\\ x-2y & < 8 \end{cases}}$
Should not have chosen
$\displaystyle{(S)\begin{cases} 2x+y & > 5\\ x-2y & > 8 \end{cases}}$
Should not have chosen
Question 4

Considérons le système suivant :
$\displaystyle (S)\begin{cases} 2x+y & = 10 \\ 3x-y & = 5 \end{cases}$
Quelle est la valeur de la solution $x$ ?

Catégorie:

CommentaireBonne réponse
3
Question 5

Soit $f$ une fonction numérique définie sur l'intervalle $[-1;3]$ et $a$ un réel de cet intervalle.
Si $f$ est continue sur $[-1;1]$ et sur $[1;3]$ alors $f$ est continue sur $[-1;3]$.

Catégorie:

Votre réponseChoixCommentaireBonne réponse
Vrai
Should have chosen
Faux
$f$ est définie sur l'intervalle $[-1;3]$.
De plus les deux intervalles $[-1;1]$ et $[1;3]$ se chevauchent.
Enfin, autour du point $x=1$, on pose $f(1)=a$, il ne reste qu'à comparer la limite à droite et à gauche de $f(x)$ avec la valeur de $f(1)=a$.
Question 6

Soit $f$ la fonction définie sur $\mathbb{R}$ par $f(x)=(2x^2+3)^3$. La fonction dérivée de $f$ est :

Catégorie:

Votre réponseChoixCommentaireBonne réponse
$f' : x \mapsto 12x(2x^2+3)^2$
Should have chosen
$f' \: x \mapsto 6(2x^2+3)^2$
$f' : x \mapsto 3(2x^2+3)^2$
Question 7

Voici la courbe représentative d'une fonction $f$ sur $[-5;5]$.
Par lecture graphique, cocher les propositions vraies :

Catégorie:

Votre réponseChoixCommentaireBonne réponse
La fonction $f$ n'est pas continue en $x=2$.
Should have chosen
La fonction $f$ est continue en $x=-2$.
La fonction $f$ est continue sur $[-2;3]$.
La fonction $f$ est continue sur $]-2;2[$
Should have chosen
La fonction $f$ est continue sur $[2;4[$.
Should have chosen
Question 8

Soit $f$ une fonction dérivable sur $\mathbb{R}$. La courbe de sa dérivée est donnée ci-dessous.
$f$ est-elle strictement décroissante sur $] -\infty ; 1 [$ ?

Catégorie:

Votre réponseChoixCommentaireBonne réponse
Vrai
Should have chosen
Faux
Quelle est le signe de $f'$ sur $] - \infty ; 1 [$ ? En déduire le sens de variation de $f$.
Question 9

Soit $f$ une fonction dérivable sur $\mathbb{R}$. La courbe de sa dérivée est donnée ci-dessous.
$f$ admet-elle un maximum en $x=2$ ?

Catégorie:

Votre réponseChoixCommentaireBonne réponse
Vrai
Faux
Should have chosen
C'est le maximum de $f'$, pas de $f$.
Question 10

La fonction dérivée de $x \mapsto \sqrt{x^2 + 1}$ est toujours positive.

Catégorie:

Votre réponseChoixCommentaireBonne réponse
Vrai
Faux
Should have chosen
Quelles sont les limites en $-\infty$ et $+\infty$ ? La monotonie est-elle possible ?
Question 11

Cette affirmation est-elle vraie ou fausse ?
Il existe un réel $a$ et un réel $b$ tels que $2e^{a+b} = e^{2a} + e^{2b}$.

Catégorie:

Votre réponseChoixCommentaireBonne réponse
Vrai
Should have chosen
Faux
Que se passe-t-il pour $a=0$ et $b=0$ ?
Question 12

Soit $f$ la fonction définie sur $\mathbb{R}$ par: $f(x)=(x+1)e^{2x}$.
Pour tout réel $x$, on a :

Catégorie:

Votre réponseChoixCommentaireBonne réponse
$f'(x)-2f(x)=e^{2x}$
Should have chosen
$f'(x) = 2(x+1)f(x)$
Should not have chosen
$f'(x)=2f(x)$
Should not have chosen
Question 13

L'expression $-e^{-x}$ :

Catégorie:

Votre réponseChoixCommentaireBonne réponse
n'est jamais négative.
Should not have chosen
n'est négative que si $x$ est négatif.
Should not have chosen
n'est négative que si $x$ est positif.
Should not have chosen
est toujours négative.
Should have chosen
Question 14

$\displaystyle \lim\limits_{x \to +\infty} \frac{2e^x+1}{e^x+2}$ est égale à :

Catégorie:

Votre réponseChoixCommentaireBonne réponse
$\displaystyle -\frac{1}{2} $
Should not have chosen
$2$
Should have chosen
$1$
Should not have chosen
$+\infty$
Should not have chosen
Question 15

L'équation $e^x=2$ a pour solution :

Catégorie:

Votre réponseChoixCommentaireBonne réponse
$\ln(2)$
Should have chosen
$\ln\left(\dfrac{1}{2}\right)$
Should not have chosen
$e^2$
Should not have chosen
Question 16

L'inéquation $e^x\leq 4$ a pour solution :

Catégorie:

Votre réponseChoixCommentaireBonne réponse
$\left] 0 ; 4 \right]$
Should not have chosen
$\left] 0 ; \ln(4) \right]$
Should not have chosen
$\left] -\infty ; \ln(4) \right]$
Should have chosen
Question 17

L'inégalité $\ln (x-1) < 1$ est vérifiée pour :

Catégorie:

Votre réponseChoixCommentaireBonne réponse
$x<1+e$
Should not have chosen
$x>1$
Should not have chosen
$1 < x < 1+e$
Should have chosen
Question 18

L'égalité $\displaystyle e^{\ln x}=x$ est vrai pour tout $x$ appartenant à :

Catégorie:

Votre réponseChoixCommentaireBonne réponse
$\left]0;+\infty\right[$
Should have chosen
$\mathbb{R}$
Should not have chosen
$\left[0;+\infty\right[$
Should not have chosen
Question 19

Ce diagramme représente la répartition du nombre de buts marqués par match pour une équipe de football tout au long du championnat.

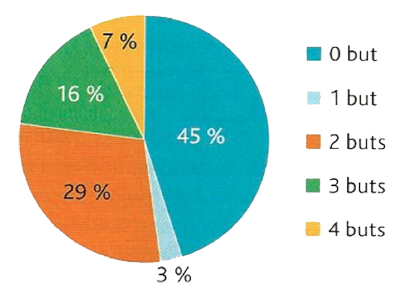
Le nombre moyen de buts marqués par match au cours du championnat est :

Catégorie:

Votre réponseChoixCommentaireBonne réponse
$\overline{x} = 1,37$
Should have chosen
$\overline{x} = 2$
Should not have chosen

On ne peut pas savoir.

Should not have chosen
$\overline{x} = 0,5$
Should not have chosen
On obtient ce résultat en faisant :
$\overline{x} = 0×0,45+1 \times 0,03+2 \times 0,29+3 \times 0,16+4 \times 0,07=1,37$
Question 20

Ce diagramme représente les fréquences (en nombre décimal de 0 à 1) en fonction des valeurs d'un caractère.

Calculer la moyenne de la série.

Catégorie:

Votre réponseChoixCommentaireBonne réponse
$\overline{x} = 108,75$
Should have chosen
$e = 0,3$
Should not have chosen
$\overline{x} = 108$
Should not have chosen

On ne peut pas savoir.

Should not have chosen
$\overline{x} = 80 \times 0,25 + 90 \times 0,1 + 105 \times 0,3 + 120 \times 0,1 + 145 \times 0,25 = 108,75$