Quiz de prérentrée

Primary tabs

Question 1

Quelle est la valeur de cette limite ?

$\displaystyle \lim_{x\to +\infty} \dfrac{1-x^3}{x^2-2}$

Catégorie:

Domaine de définition

Votre réponse	Choix	Commentaire	Bonne réponse
	$1$	Mettre le terme de plus haute puissance $x^3$ en facteur au numérateur et au dénominateur, puis simplifier.
	$-\infty$
	$+\infty$
	$0$

Question 2

Quel est le domaine de définition dans

$\mathbb{R}$ de la fonction suivante :

$\dfrac{x+1}{\sqrt{x^2-1}}$

Catégorie:

Domaine de définition

Votre réponse	Choix	Commentaire	Bonne réponse
	$\rbrack -1 ; 1 \lbrack$
	$\rbrack -\infty ; -1 \lbrack \; \cup \; \rbrack 1 ; +\infty \lbrack$
	$\rbrack -\infty ; -1 \rbrack \; \cup \; \lbrack 1 ; +\infty \lbrack$
	$\mathbb{R} \setminus \{ -1 ; 1 \}$

Question 3

À quel système correspond la région blanche du graphique ?

Catégorie:

Systèmes d'équations, inéquations, 2nd degré

Votre réponse	Choix	Commentaire	Bonne réponse
	$\displaystyle{(S)\begin{cases} 2x+y & > 5\\ x-2y & < 8 \end{cases}}$
	$\displaystyle{(S)\begin{cases} 2x+y & < 5\\ x-2y & < 8 \end{cases}}$
	$\displaystyle{(S)\begin{cases} 2x+y & > 5\\ x-2y & > 8 \end{cases}}$
	$\displaystyle{(S)\begin{cases} 2x+y & < 5\\ x-2y & > 8 \end{cases}}$

Question 4

Considérons le système suivant :

$\displaystyle (S)\begin{cases} 2x+y & = 10 \\ 3x-y & = 5 \end{cases}$
Quelle est la valeur de la solution

$x$ ?

Catégorie:

Systèmes d'équations, inéquations, 2nd degré

Votre réponse	Commentaire	Bonne réponse
3		3

Question 5

La fonction

$x \mapsto x\sqrt{x}$ est dérivable en

$x=0$ .

Catégorie:

Continuité et dérivation

Votre réponse	Choix	Commentaire	Bonne réponse
	Vrai
	Faux

Revenir à la définition de la dérivée et calculer la limite en

$x=0$ de

$\lim\limits_{h\to 0 \\ h>0} \frac{(x+h)\sqrt{x+h}}{h}$ .

Question 6

Soit

$f$ une fonction numérique définie sur l'intervalle

$[-1;3]$ et

$a$ un réel de cet intervalle.
Si

$f$ est continue sur

$[-1;1]$ et sur

$[1;3]$ alors

$f$ est continue sur

$[-1;3]$ .

Catégorie:

Continuité et dérivation

Votre réponse	Choix	Commentaire	Bonne réponse
	Vrai
	Faux

$f$ est définie sur l'intervalle

$[-1;3]$ .
De plus les deux intervalles

$[-1;1]$ et

$[1;3]$ se chevauchent.
Enfin, autour du point

$x=1$ , on pose

$f(1)=a$ , il ne reste qu'à comparer la limite à droite et à gauche de

$f(x)$ avec la valeur de

$f(1)=a$ .

Question 7

La fonction

$x \mapsto x\sqrt{x}$ est dérivable en

$x=0$ .

Catégorie:

Continuité et dérivation

Votre réponse	Choix	Commentaire	Bonne réponse
	Vrai
	Faux

Revenir à la définition de la dérivée et calculer la limite en

$x=0$ de

$\lim\limits_{\substack{h\to 0 \\ h>0}} \frac{(x+h)\sqrt{x+h}}{h}$ .

Question 8

La fonction dérivée de

$x \mapsto \sqrt{x^2 + 1}$ est toujours positive.

Catégorie:

Étude de fonctions

Votre réponse	Choix	Commentaire	Bonne réponse
	Vrai
	Faux

Quelles sont les limites en

$-\infty$ et

$+\infty$ ? La monotonie est-elle possible ?

Question 9

Soit

$f$ une fonction dérivable sur

$\mathbb{R}$ . La courbe de sa dérivée est donnée ci-dessous.

$f$ est-elle strictement décroissante sur

$] -\infty ; 1 [$ ?

Catégorie:

Étude de fonctions

Votre réponse	Choix	Commentaire	Bonne réponse
	Vrai
	Faux

Quelle est le signe de

$f'$ sur

$] - \infty ; 1 [$ ? En déduire le sens de variation de

$f$ .

Question 10

Soit

$f$ une fonction numérique et

$\mathcal{C}_f$ sa courbe représentative dans le plan muni du repère

$(O ; \vec{i} ; \vec{j} )$ .
Si la tangente à

$\mathcal{C}_f$ au point

$B(1 ; 5 )$ est parallèle à la droite d'équation

$y=2x + 1$ alors

$f'(1)=2$ .

Catégorie:

Étude de fonctions

Votre réponse	Choix	Commentaire	Bonne réponse
	Vrai
	Faux

La tangente en

$B( 1 ; 5 )$ parallèle à

$y=2x + 1$ permet d'obtenir son coefficient directeur. Le coefficient directeur permet de déduire le nombre dérivé

$f'(1)$ .

Question 11

Cette formule est-elle vraie ou fausse ?
Pour tous réels

$a$ et

$b$ ,

$e^{a+b}=\sqrt{e^{2a}e^{2b}}$ .

Catégorie:

Exponentielle

Votre réponse	Choix	Commentaire	Bonne réponse
	Vrai
	Faux

Revoir ses formules classiques :

$\sqrt{a\times b} = \sqrt{a}\times \sqrt{b}$

$\sqrt{X} = X^{\frac{1}{2}}$

$e^a\times e^b = e^{a+b}$

${e^a}^b = e^{a\times b}$

Question 12

Dans

$\mathbb{R}$ , l'équation

$e^{2x}-3e^x - 4=0$ admet :

Catégorie:

Exponentielle

Votre réponse	Choix	Commentaire	Bonne réponse
	Une seule solution.
	Deux solutions.
	Aucune solution.

Question 13

Soit

$f$ la fonction définie sur

$\mathbb{R}$ par:

$f(x)=(x+1)e^{2x}$ .
Pour tout réel

$x$ , on a :

Catégorie:

Exponentielle

Votre réponse	Choix	Commentaire	Bonne réponse
	$f'(x) = 2(x+1)f(x)$
	$f'(x)=2f(x)$
	$f'(x)-2f(x)=e^{2x}$

Question 14

Soit

$f$ la fonction définie sur

$\mathbb{R}$ par:

$\displaystyle f(x)=(x+1)e^{2x}$ .
L'équation

$f(x)=1$ admet dans

$\mathbb{R}$ :

Catégorie:

Exponentielle

Votre réponse	Choix	Commentaire	Bonne réponse
	deux solutions.
	aucune solution.	Étudier la fonction $f(x)$ et dresser le tableau de variation.
	une unique solution.

Question 15

L'équation

$e^x=2$ a pour solution :

Catégorie:

Logarithmes

Votre réponse	Choix	Commentaire	Bonne réponse
	$\ln\left(\dfrac{1}{2}\right)$
	$e^2$
	$\ln(2)$

Question 16

L'inéquation

$e^x\leq 4$ a pour solution :

Catégorie:

Logarithmes

Votre réponse	Choix	Commentaire	Bonne réponse
	$\left] 0 ; \ln(4) \right]$	Revoir le domaine de définition de $x\mapsto e^x$ .
	$\left] -\infty ; \ln(4) \right]$
	$\left] 0 ; 4 \right]$

Question 17

La représentation graphique de la fonction logarithme népérien admet :

Catégorie:

Logarithmes

Votre réponse	Choix	Commentaire	Bonne réponse
	une tangente horizontale.
	une asymptote verticale.
	une asymptote horizontale.

Question 18

L'égalité

$\displaystyle e^{\ln x}=x$ est vrai pour tout

$x$ appartenant à :

Catégorie:

Logarithmes

Votre réponse	Choix	Commentaire	Bonne réponse
	$\mathbb{R}$	Revoir le domaine de définition de $x \mapsto \ln(x)$ .
	$\left]0;+\infty\right[$
	$\left[0;+\infty\right[$

Question 19

Voici la courbe des fréquences cumulées croissantes du nombre d'enfants moyen par famille en France en 2007.

Parmi les 4 affirmations suivantes, laquelle est correcte ?

Catégorie:

Statistiques

Votre réponse	Choix	Commentaire	Bonne réponse
	22 % des familles ont un enfant unique.
	3 % des familles ont au plus 3 enfants.
	90 % des familles ont au moins 2 enfants.
	70 % des familles ont au moins 1 enfant.

Pour trouver la fréquence des familles ayant un seul enfant, on fait le calcul

$0,7 - 0,48 = 0,22$ .

Question 20

Ce diagramme représente les fréquences (en nombre décimal de 0 à 1) en fonction des valeurs d'un caractère.

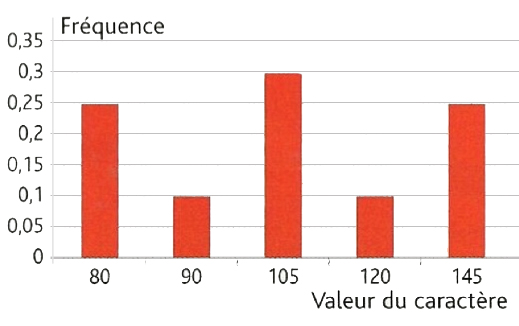
Calculer la moyenne de la série.

Catégorie:

Statistiques

Votre réponse	Choix	Commentaire	Bonne réponse
	$\overline{x} = 108,75$
	$e = 0,3$
	$\overline{x} = 108$
	On ne peut pas savoir.

$\overline{x} = 80 \times 0,25 + 90 \times 0,1 + 105 \times 0,3 + 120 \times 0,1 + 145 \times 0,25 = 108,75$

Main menu

Quiz de prérentrée

Primary tabs

Catégorie:

Catégorie:

Catégorie:

Catégorie:

Catégorie:

Catégorie:

Catégorie:

Catégorie:

Catégorie:

Catégorie:

Catégorie:

Catégorie:

Catégorie:

Catégorie:

Catégorie:

Catégorie:

Catégorie:

Catégorie:

Catégorie:

Catégorie: