Quiz de prérentrée

Primary tabs

Question 1

Quelle est la valeur de cette limite ? $\displaystyle \lim_{x\to +\infty} \sqrt{x+1}-\sqrt{x}$

Catégorie:

Votre réponseChoixCommentaireBonne réponse
$+\infty$
Should not have chosen
$0$
Should have chosen
$-\infty$
Should not have chosen
Selected
$1$
Utiliser la quantité conjuguée de $\sqrt{x+1}-\sqrt{x}$. Multiplier par $\dfrac{\sqrt{x+1}+\sqrt{x}}{\sqrt{x+1}+\sqrt{x}}$.
Should not have chosen
Question 2

Quel est le domaine de définition dans $\mathbb{R}$ de la fonction suivante : $\dfrac{x^2-1}{x^2+1}$

Catégorie:

Votre réponseChoixCommentaireBonne réponse
$\lbrack -1 ; 1 \rbrack $
Should not have chosen
$\mathbb{R} \setminus \{ -1; 1 \}$
Should not have chosen
$\rbrack -\infty ; -1 \lbrack \; \cup \; \rbrack 1 ; +\infty \lbrack$
Should not have chosen
Selected
$\mathbb{R}$
Should have chosen
Question 3

À quel système correspond la région blanche du graphique ?

Catégorie:

Votre réponseChoixCommentaireBonne réponse
$\displaystyle{(S)\begin{cases} 2x+y & < 5\\ x-2y & < 8 \end{cases}}$
Should not have chosen
$\displaystyle{(S)\begin{cases} 2x+y & < 5\\ x-2y & > 8 \end{cases}}$
Should have chosen
$\displaystyle{(S)\begin{cases} 2x+y & > 5\\ x-2y & < 8 \end{cases}}$
Should not have chosen
Selected
$\displaystyle{(S)\begin{cases} 2x+y & > 5\\ x-2y & > 8 \end{cases}}$
C'est la région bleue. Il suffit de tester le point $(x=5 ; y=-2)$.
Should not have chosen
Question 4

Considérons le système suivant :
$\displaystyle (S)\begin{cases} 2x+y & = 10 \\ 3x-y & = 5 \end{cases}$
Quelle est la valeur de la solution $x$ ?

Catégorie:

CommentaireBonne réponse
3
Question 5

Voici la courbe représentative d'une fonction $f$ sur $[-5;5]$.
Par lecture graphique, cocher les propositions vraies :

Catégorie:

Votre réponseChoixCommentaireBonne réponse
La fonction $f$ n'est pas continue en $x=2$.
Should have chosen
La fonction $f$ est continue en $x=-2$.
La fonction $f$ est continue sur $[-2;3]$.
La fonction $f$ est continue sur $]-2;2[$
Should have chosen
Selected
La fonction $f$ est continue sur $[2;4[$.
Should have chosen
Question 6

Soit $f$ une fonction numérique définie sur l'intervalle $[-1;3]$ et $a$ un réel de cet intervalle.
Si $f$ est continue sur $[-1;1]$ et sur $[1;3]$ alors $f$ est continue sur $[-1;3]$.

Catégorie:

Votre réponseChoixCommentaireBonne réponse
Selected
Vrai
Should have chosen
Faux
$f$ est définie sur l'intervalle $[-1;3]$.
De plus les deux intervalles $[-1;1]$ et $[1;3]$ se chevauchent.
Enfin, autour du point $x=1$, on pose $f(1)=a$, il ne reste qu'à comparer la limite à droite et à gauche de $f(x)$ avec la valeur de $f(1)=a$.
Question 7

Soit $f$ la fonction définie sur $\mathbb{R}$ par $f(x)=(2x^2+3)^3$. La fonction dérivée de $f$ est :

Catégorie:

Votre réponseChoixCommentaireBonne réponse
$f' : x \mapsto 12x(2x^2+3)^2$
Should have chosen
Selected
$f' \: x \mapsto 6(2x^2+3)^2$
Erreur de calcul. Revoir la règle de calcul de la dérivée des fonctions composées : $u(v(x))' = v'(x) \times u'(v(x))$.
$f' : x \mapsto 3(2x^2+3)^2$
Question 8

Soit $f$ une fonction numérique et $\mathcal{C}_f$ sa courbe représentative dans le plan muni du repère $(O ; \vec{i} ; \vec{j} )$.
Si la tangente à $\mathcal{C}_f$ au point $B(1 ; 5 )$ est parallèle à la droite d'équation $y=2x + 1$ alors $f'(1)=2$.

Catégorie:

Votre réponseChoixCommentaireBonne réponse
Selected
Vrai
Should have chosen
Faux
La tangente en $B( 1 ; 5 )$ parallèle à $y=2x + 1$ permet d'obtenir son  coefficient directeur. Le coefficient directeur permet de déduire le nombre dérivé $f'(1)$.
Question 9

Soit $f$ une fonction dérivable sur $\mathbb{R}$. La courbe de sa dérivée est donnée ci-dessous.
$f$ est-elle strictement décroissante sur $] -\infty ; 1 [$ ?

Catégorie:

Votre réponseChoixCommentaireBonne réponse
Vrai
Should have chosen
Selected
Faux
Quelle est le signe de $f'$ sur $] - \infty ; 1 [$ ? En déduire le sens de variation de $f$.
Question 10

Soit $f$ une fonction dérivable sur $\mathbb{R}$. La courbe de sa dérivée est donnée ci-dessous.
$f$ admet-elle un minimum en $x=1$ ?

Catégorie:

Votre réponseChoixCommentaireBonne réponse
Selected
Vrai
Should have chosen
Faux
Étudier le signe de $f'$ à gauche et à droite de $x=1$. En déduire le sens de variation de $f$ et conclure sur la nature du point de la courbe de $f$ d'abscisse $x=1$.
Question 11

Soient $f$ et $g$ les fonctions définies sur $\mathbb{R}$ par : $f(x)=(x+1)e^{2x}$ et $\displaystyle g(x)=\frac{1-x}{e^{2x}}$. On a :

Catégorie:

Votre réponseChoixCommentaireBonne réponse
$\lim \limits_{x \to -\infty} \left( f\left(x\right) +g\left(x\right) \right)= +\infty$
Should have chosen
$\lim \limits_{x \to -\infty} f(x) = -\infty$
Should not have chosen
$\lim \limits_{x \to -\infty} g(x) = 0$
Should not have chosen
Question 12

L'expression $e^x(2e^{-x}-1)$ est égale à :

Catégorie:

Votre réponseChoixCommentaireBonne réponse
$2-e^x$
Should have chosen
$2e^{-x^2}-e^x$
Should not have chosen
$-2(e^x)^2-e^x$
Should not have chosen
Question 13

$\displaystyle \lim\limits_{x \to +\infty} \frac{2e^x+1}{e^x+2}$ est égale à :

Catégorie:

Votre réponseChoixCommentaireBonne réponse
$+\infty$
Should not have chosen
$\displaystyle -\frac{1}{2} $
Should not have chosen
$1$
Should not have chosen
Selected
$2$
Should have chosen
Question 14

Dans $\mathbb{R}$, l'équation $e^{2x}-3e^x - 4=0$ admet :

Catégorie:

Votre réponseChoixCommentaireBonne réponse

Aucune solution.

Should not have chosen
Deux solutions.
Should not have chosen
Selected
Une seule solution.
Should have chosen
Question 15

L'équation $e^x=2$ a pour solution :

Catégorie:

Votre réponseChoixCommentaireBonne réponse
Selected
$e^2$
Utiliser la fonction réciproque $x \mapsto \ln (x)$.
Should not have chosen
$\ln\left(\dfrac{1}{2}\right)$
Should not have chosen
$\ln(2)$
Should have chosen
Question 16

Soit $f$ la fonction définie sur $]0 ; +\infty [ $ par $f(x)=x^2\ln(x)$.
Le nombre dérivé de $f$ en $e$ est :

Catégorie:

Votre réponseChoixCommentaireBonne réponse
Selected
$0$
Revoir $\ln'(x)=\frac{1}{x}$ et $\left(uv\right)'(x)=u'(x)v(x) + u(x)v'(x)$.
Should not have chosen
$3e$
Should have chosen
$e^2$
Should not have chosen
Question 17

L'égalité $\displaystyle e^{\ln x}=x$ est vrai pour tout $x$ appartenant à :

Catégorie:

Votre réponseChoixCommentaireBonne réponse
Selected
$\mathbb{R}$
Revoir le domaine de définition de $x \mapsto \ln(x)$.
Should not have chosen
$\left[0;+\infty\right[$
Should not have chosen
$\left]0;+\infty\right[$
Should have chosen
Question 18

Soit $f$ la fonction définie par $f(x)=\ln\left(x^2\right)$.
L'ensemble de définition de $f$ est :

Catégorie:

Votre réponseChoixCommentaireBonne réponse
$\mathbb{R}^*$
Should have chosen
$\mathbb{R}$
Should not have chosen
Selected
$]0;+\infty [$
Que se passe-t-il pour $x=-1$ ?
Il faut résoudre $x^2>0$.
Should not have chosen
Question 19

Ce tableau représente le nombre de fichiers mp3 installés dans les lecteurs mp3 des élèves d'une classe de 20 élèves.

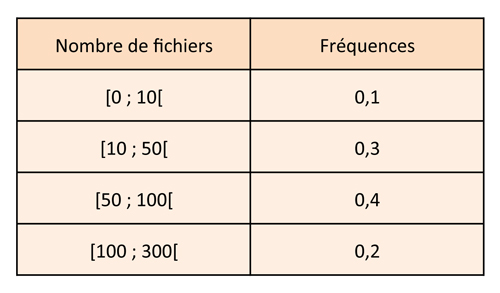
La moyenne des fichiers est :

Catégorie:

Votre réponseChoixCommentaireBonne réponse
$\overline{x} = 43$
Should not have chosen
Selected
$\overline{x} = 79,5$
Should have chosen
$\overline{x} = 116$
Should not have chosen
On ne peut pas savoir.
Should not have chosen
Le principe lorsque l'on a un regroupement par classe est de remplacer chaque classe par son centre : le centre de la classe $[0;10[$ est 5, le centre de la classe $[10;50[$ est 30, le centre de la classe $[50;100[$ est 75, etc.
Ensuite on fait la moyenne de la série :
$\overline{x} = 5 \times 0,1 + 30 \times 0,3 + 75 \times 0,4 + 200 \times 0,2 = 79,5$
Question 20

Ce diagramme représente la répartition des élèves d'un lycée qui accueille 286 élèves en Seconde.

Quelle est la proportion $\frac{post-bac}{première}$ ?

Catégorie:

Votre réponseChoixCommentaireBonne réponse

On ne peut pas savoir.

Should not have chosen
$\frac{1}{3}$
Should not have chosen
$\frac{3}{8}$
Should have chosen
$\frac{3}{7}$
Should not have chosen
Le pourcentage d'élèves en post-bac est égal à $100-(32,5+26,25+30) = 11,25 %$.
La proportion demandée est donc $\frac{11,25}{30}=0,375=\frac{3}{8}$.