Quiz de prérentrée

Primary tabs

Question 1

Quel est le domaine de définition dans $\mathbb{R}$ de la fonction suivante : $\dfrac{x+1}{\sqrt{x^2-1}}$

Catégorie:

Domaine de définition

Votre réponse	Choix	Commentaire	Bonne réponse
	$\rbrack -1 ; 1 \lbrack$
	$\rbrack -\infty ; -1 \lbrack \; \cup \; \rbrack 1 ; +\infty \lbrack$
	$\rbrack -\infty ; -1 \rbrack \; \cup \; \lbrack 1 ; +\infty \lbrack$	Pour $x\=-1$ ou $x\=1$ le dénominateur $\sqrt{x^2-1}$ est nul et la fraction n'est donc pas définie.
	$\mathbb{R} \setminus \{ -1 ; 1 \} $

Question 2

Quelle est la valeur de cette limite ? $\displaystyle \lim_{x\to +\infty} \sqrt{x+1}-\sqrt{x}$

Catégorie:

Domaine de définition

Votre réponse	Choix	Commentaire	Bonne réponse
	$-\infty$
	$+\infty$
	$1$
	$0$

Question 3

À quel système correspond la région blanche du graphique ?

Catégorie:

Systèmes d'équations, inéquations, 2nd degré

Votre réponse	Choix	Commentaire	Bonne réponse
	$\displaystyle{(S)\begin{cases} 2x+y & < 5\\ x-2y & > 8 \end{cases}}$
	$\displaystyle{(S)\begin{cases} 2x+y & < 5\\ x-2y & < 8 \end{cases}}$
	$\displaystyle{(S)\begin{cases} 2x+y & > 5\\ x-2y & > 8 \end{cases}}$
	$\displaystyle{(S)\begin{cases} 2x+y & > 5\\ x-2y & < 8 \end{cases}}$

Question 4

Considérons un système général de 2 équations à 2 inconnues: $\displaystyle (S)\begin{cases} a\times x + b\times y &= c\\ \alpha\times x + \beta\times y &= \gamma \end{cases} $
Soit $E$ l'ensemble des solutions de $(S)$. Combien de solutions possibles peut comporter l'ensemble $E$ ?

Catégorie:

Systèmes d'équations, inéquations, 2nd degré

Votre réponse	Choix	Commentaire	Bonne réponse
	Une seule solution. Système régulier.	$\displaystyle (S)\begin{cases} x + y &= 0\\ x - y &= 2\end{cases}$ $E=\left\{ ( x=1 ; y=-1) \right\}$
	Aucune solution. Système incompatible.
	Exactement deux solutions.
	Une infinité de solutions. Système lié.

Question 5

Soit $f$ une fonction numérique définie sur l'intervalle $[-1;3]$ et $a$ un réel de cet intervalle.
Si $f$ est dérivable en $a$ elle est continue en $a$.

Catégorie:

Continuité et dérivation

Votre réponse	Choix	Commentaire	Bonne réponse
	Vrai
	Faux

C'est un théorème du cours.

Question 6

Voici la courbe représentative d'une fonction $f$ sur $[-5;5]$.

Par lecture graphique, cocher les propositions vraies :

Catégorie:

Continuité et dérivation

Votre réponse	Choix	Commentaire	Bonne réponse
	La fonction $f$ n'est pas continue en $x=2$.
	La fonction $f$ est continue en $x=-2$.
	La fonction $f$ est continue sur $[-2;3]$.
	La fonction $f$ est continue sur $]-2;2[$
	La fonction $f$ est continue sur $[2;4[$.

Question 7

La fonction $x \mapsto x\sqrt{x}$ est dérivable en $x=0$.

Catégorie:

Continuité et dérivation

Votre réponse	Choix	Commentaire	Bonne réponse
	Vrai
	Faux

Revenir à la définition de la dérivée et calculer la limite en $x=0$ de $\lim\limits_{\substack{h\to 0 \\ h>0}} \frac{(x+h)\sqrt{x+h}}{h}$.

Question 8

Soit $f$ une fonction dérivable sur $\mathbb{R}$. La courbe de sa dérivée est donnée ci-dessous.
$f$ admet-elle un maximum en $x=2$ ?

Catégorie:

Étude de fonctions

Votre réponse	Choix	Commentaire	Bonne réponse
	Vrai
	Faux

C'est le maximum de $f'$, pas de $f$.

Question 9

Soit $f$ une fonction numérique et $\mathcal{C}_f$ sa courbe représentative dans le plan muni du repère $(O ; \vec{i} ; \vec{j} )$.
Si la tangente à la courbe $\mathcal{C}_f$ au point $A(0 ; 2)$ est la droite d'équation $y=2$ alors $f'(0)=2$.

Catégorie:

Étude de fonctions

Votre réponse	Choix	Commentaire	Bonne réponse
	Vrai
	Faux

La tangente en $x=0$ est-elle horizontale ? Si oui, que vaut $f'(0)$ ?

Question 10

Soit $L$ une fonction définie et dérivable sur $]0 ; +\infty [$ telle que pour tout réel $x$ de $]0; +\infty[$, $L'(x) = \dfrac{1}{x}$ et $L(1)=0$.
Alors la fonction $L$ est négative sur $] 0 ; 1 [$ et positive sur $]1 ; +\infty [$

Catégorie:

Étude de fonctions

Votre réponse	Choix	Commentaire	Bonne réponse
	Vrai
	Faux

À partir de l'énoncé, dresser le tableau de signe de $L'$ en déduire le sens de variation de $L$ en inscrivant la valeur de $L(1)=0$.

Question 11

Cette formule est-elle vraie ou fausse ?
Pour tous réels $a$ et $b$, $e^{a+b}=\sqrt{e^{2a}e^{2b}}$.

Catégorie:

Exponentielle

Votre réponse	Choix	Commentaire	Bonne réponse
	Vrai
	Faux

Revoir ses formules classiques :
$\sqrt{a\times b} = \sqrt{a}\times \sqrt{b}$
$\sqrt{X} = X^{\frac{1}{2}}$
$e^a\times e^b = e^{a+b}$
${e^a}^b = e^{a\times b}$

Question 12

$\displaystyle\lim\limits_{x \to +\infty} e^{-2x^2}$ est égale à :

Catégorie:

Exponentielle

Votre réponse	Choix	Commentaire	Bonne réponse
	$0$
	$+\infty$
	$-\infty$

Question 13

Soient $f$ et $g$ les fonctions définies sur $\mathbb{R}$ par : $f(x)=(x+1)e^{2x}$ et $\displaystyle g(x)=\frac{1-x}{e^{2x}}$. On a :

Catégorie:

Exponentielle

Votre réponse	Choix	Commentaire	Bonne réponse
	$\lim \limits_{x \to -\infty} f(x) = -\infty$
	$\lim \limits_{x \to -\infty} \left( f\left(x\right) +g\left(x\right) \right)= +\infty$
	$\lim \limits_{x \to -\infty} g(x) = 0$

Question 14

Soit $f$ la fonction définie sur $\mathbb{R}$ par: $\displaystyle f(x)=(x+1)e^{2x}$.
L'équation $f(x)=1$ admet dans $\mathbb{R}$ :

Catégorie:

Exponentielle

Votre réponse	Choix	Commentaire	Bonne réponse
	deux solutions.
	une unique solution.
	aucune solution.

Question 15

L'équation $e^x=-2$ a pour solution :

Catégorie:

Logarithmes

Votre réponse	Choix	Commentaire	Bonne réponse
	$\ln(2)$
	$\ln (-2)$
	aucune

Question 16

L'inéquation $e^x\leq 4$ a pour solution :

Catégorie:

Logarithmes

Votre réponse	Choix	Commentaire	Bonne réponse
	$\left] -\infty ; \ln(4) \right]$
	$\left] 0 ; \ln(4) \right]$
	$\left] 0 ; 4 \right]$

Question 17

L'équation $e^x=2$ a pour solution :

Catégorie:

Logarithmes

Votre réponse	Choix	Commentaire	Bonne réponse
	$e^2$
	$\ln(2)$
	$\ln\left(\dfrac{1}{2}\right)$

Question 18

La représentation graphique de la fonction logarithme népérien admet :

Catégorie:

Logarithmes

Votre réponse	Choix	Commentaire	Bonne réponse
	une tangente horizontale.
	une asymptote horizontale.
	une asymptote verticale.

Question 19

Ce diagramme représente les fréquences (en nombre décimal de 0 à 1) en fonction des valeurs d'un caractère.

Calculer la moyenne de la série.

Catégorie:

Statistiques

Votre réponse	Choix	Commentaire	Bonne réponse
	$\overline{x} = 108,75$
	$e = 0,3$
	On ne peut pas savoir.
	$\overline{x} = 108$

$\overline{x} = 80 \times 0,25 + 90 \times 0,1 + 105 \times 0,3 + 120 \times 0,1 + 145 \times 0,25 = 108,75$

Question 20

Ce nuage de points représente les fréquences cumulées croissantes d'une série statistique constituée par les salaires mensuels, en centaines d'euros, des salariés d'une entreprise.

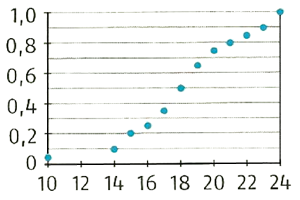
Une seule des 4 affirmations suivantes est correcte. Laquelle ?

Catégorie:

Statistiques

Votre réponse	Choix	Commentaire	Bonne réponse
	La moitié au moins des salaires mensuels sont supérieurs ou égaux à 1 900 euros.
	La moitié au moins des salaires mensuels est comprise entre 1 600 euros et 2 000 euros inclus.
	On ne peut pas savoir.
	Trois-quarts des salaires mensuels sont inférieurs à 1 900 euros.

Déjà, le salaire correspondant à une fréquence de $0,75$ est de 2000 euros (et pas 1900) : l'affirmation "Trois-quarts des salaires mensuels sont inférieurs à 1 900 euros." est fausse. De même, l'affirmation "La moitié au moins des salaires mensuels sont supérieurs ou égaux à 1 900 euros." est fausse car la moitié des salaires est inférieure à 1800 euros. Le salaire 1 600 euros a une fréquence de $0,25$, et le salaire 2000 euros a une fréquence de $0,75$ : donc, comme entre $0,25$ et $0,75$, on a 50 % des effectifs, il vient que la moitié au moins des salaires est comprise entre 1 600 euros et 2 000 euros inclus.

Main menu

Quiz de prérentrée

Primary tabs

Catégorie:

Catégorie:

Catégorie:

Catégorie:

Catégorie:

Catégorie:

Catégorie:

Catégorie:

Catégorie:

Catégorie:

Catégorie:

Catégorie:

Catégorie:

Catégorie:

Catégorie:

Catégorie:

Catégorie:

Catégorie:

Catégorie:

Catégorie: